最終更新日:2023年09月05日
インスタ用にデータ更新しました。(n=2220→2573)
注文して ラーメン が提供されるまでの待ち時間、短い程ありがたいのは間違いないですけど、そこはお店の都合も有るのでしょう。
最近ではあえて行列作るために・・・という話も耳にはしますけど、着席してからは早く提供された方が嬉しいです。
実際どの程度が妥当なのでしょうか。
記録が残っている、2013年~2023年8月分までのラーメン提供時間の分布を見てみましょう。
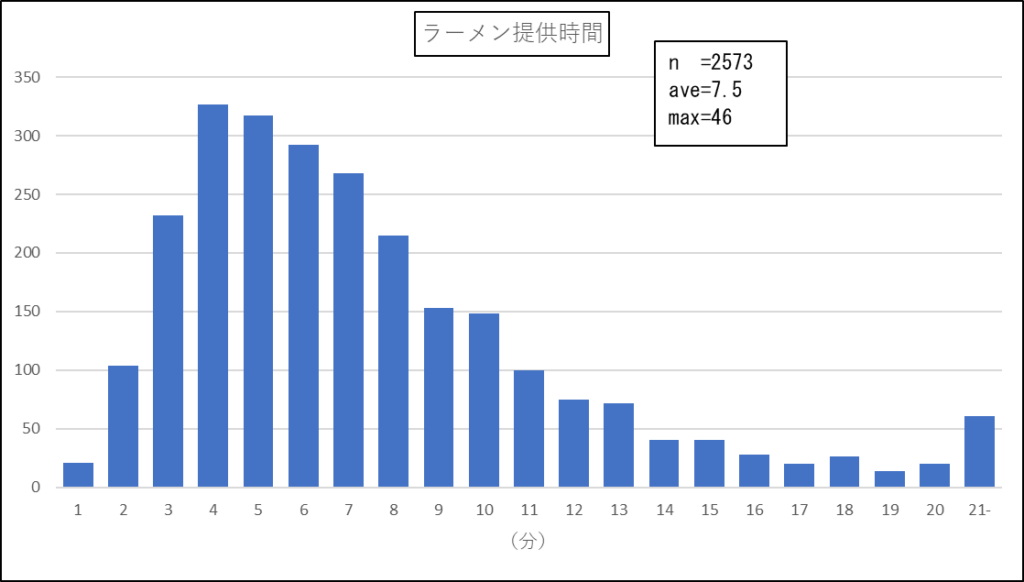
提供時間
行列に並んでいる時間は対象外。
着席して口頭オーダー又は食券を渡してからラーメンが提供されるまでの時間。
着席前に事前に食券渡す場合は、着席してからラーメンが提供されるまでの時間。
χ2分布のような形になりました。
提供時間が、30分、40分等、極端に遅いお店も少なくないので、平均値(7.5分)で考えるよりは、最頻値の「4分」で考えた方が実際の感覚とあうかもしれません。
勿論、お店の状況次第で単純に言うことはできませんが、おおよそ中央値(メジアン)の6分以内で提供されるお店が半分程のようです。
| 待ち時間 | 割合(%) |
| ~1分 | 0.8 |
| ~2分 | 4.9 |
| ~3分 | 13.9 |
| ~4分 | 26.6 |
| ~5分 | 38.9 |
| ~6分 | 50.3 |
| ~7分 | 60.7 |
ここから少しマニアックな領域になりますことご容赦。
待ち時間に関し、影響を与える因子としては、
①お店のキャパ
②オペ
③先客人数
などが考えられますが、①お店のキャパは、②と③になじんでしまうはずだと決めつけて、データのとりやすい②オペ人数と③先客の人数、それと実際に掛かった提供時間のデータを用いて重回帰分析を実施してみました。(事細かい統計の解説は省略)
| 回帰統計 | |
| 重相関 R | 0.319026 |
| 重決定 R2 | 0.101777 |
| 補正 R2 | 0.092014 |
| 標準誤差 | 3.527416 |
| 観測数 | 187 |
| 係数 | 標準誤差 | t | P-値 | 下限 95% | 上限 95% | 下限 95.0% | 上限 95.0% | |
| 切片 | 6.291529 | 0.619109 | 10.16223 | 1.54E-19 | 5.070063 | 7.512994 | 5.070063 | 7.512994 |
| 先客 | 0.275588 | 0.060392 | 4.563319 | 9.18E-06 | 0.156438 | 0.394738 | 0.156438 | 0.394738 |
| 店員 | -0.37087 | 0.244602 | -1.51623 | 0.131178 | -0.85346 | 0.111713 | -0.85346 | 0.111713 |
結果、[提供時間(分)=6.3+0.27×先客人数-0.37×オペ人数]という回帰式となりました。
ただ、店員のp値は0.13でその扱いが微妙、そもそも決定係数が0.1ととんでもないので単純に先客での単回帰がよいのかもしれませんしそもそも意味のないものだとはわかっていながらも、個人的にどうしても2つの因子をおりまぜたく、補正するというか無理くり式を作ってみたのがこちら。
[提供時間(分)=(√(先客人数^2÷オペ人数))÷0.8+3.0]
なのですが、これらは冒頭の n=2220 の分布図データからではなく、2018年5月の時点でn数も大して多くない時にあれやこれやと計算した結果なので、今一度再考してあみだしたのがこの式。
[提供時間(分)=(0.3×先客人数+1)÷(0.12×オペ人数+0.85)×3.8]
もう何がなんだかわかりませんね。
数字/統計マニアにとって、ただの趣味の世界です。
できれば、麺の太さ(太麺の方が茹で時間がかかる)や、 テボ なのか 平ザル なのか、自分が一人でオーダーしたのかグループでまとめてオーダーしたのか等の補正値も考慮した式を作ってみたくなるのは、もう変態の領域です。
というわけで、ここからは難しい式はやめにして、感覚的な話。
いわゆる官能評価の世界です。
2分や3分で提供されると「早いな」と皆様感じると思いますけど、じゃあどの程度かかると「遅いな~」と感じ始めるのか統計処理してみましょう。
やり方としては、官能評価定番の数値化。
実際にかかった時間とその時の気分を記録し、早い遅い等の感覚を数段階にわけて数値にしています。
・条件「先客 or 仕掛無し」で「被験者1名での入店時」(「2人以上で入店時」と「20分以上掛かった場合は対象外」)
n=100、R2=0.84
結果
- 2.55分以内の提供であれば「早いな」と感じる
- 2.55~6.01分での提供の場合、特に何も感じない
- 6.01分を超えると、「ん?どうしたのかな?」と感じ始める
- 9.46分を超えると「何か遅いなぁ」と感じる
- 12.9分を超えると「苛立ち始める」
というわけで、お客様にノーストレスで提供しようと思った場合、「6分」以内が望ましい という結論になりました。
2人以上で入店した場合は、提供されるまで話していればたかだか10分くらいはわけないと感じるとは思うのですが、1人でスマホイジイジして待ってる場合は、案外セッカチな結果となりました。
条件を詳細にわけたりバラエティに富んだ被験者でデータをとれば結果の信頼性はもっともっとあがりますが、これだけ見ても面白いと思うのはやはり数字マニアだけかしら。